CSQL: Mapping Documents into Causal Databases

We describe a novel system, CSQL, which automatically converts a collection of unstructured text documents into an SQL-queryable causal database (CDB). A CDB differs from a traditional DB: it is designed to answer "why'' questions via causal interventions and structured causal queries. CSQL builds on our earlier system, DEMOCRITUS, which converts documents into thousands of local causal models derived from causal discourse. Unlike RAG-based systems or knowledge-graph based approaches, CSQL supports causal analysis over document collections rather than purely associative retrieval. For example, given an article on the origins of human bipedal walking, CSQL enables queries such as: "What are the strongest causal influences on bipedalism?'' or "Which variables act as causal hubs with the largest downstream influence?'' Beyond single-document case studies, we show that CSQL can also ingest RAG/IE-compiled causal corpora at scale by compiling the Testing Causal Claims (TCC) dataset of economics papers into a causal database containing 265,656 claim instances spanning 45,319 papers, 44 years, and 1,575 reported method strings, thereby enabling corpus-level causal queries and longitudinal analyses in CSQL. Viewed abstractly, CSQL functions as a compiler from unstructured documents into a causal database equipped with a principled algebra of queries, and can be applied broadly across many domains ranging from business, humanities, and science.

Categorical Belief Propagation: Sheaf-Theoretic Inference via Descent and Holonomy

We develop a categorical foundation for belief propagation on factor graphs. We construct the free hypergraph category \(\Syn_Σ\) on a typed signature and prove its universal property, yielding compositional semantics via a unique functor to the matrix category \(\cat{Mat}_R\). Message-passing is formulated using a Grothendieck fibration \(\int\Msg \to \cat{FG}_Σ\) over polarized factor graphs, with schedule-indexed endomorphisms defining BP updates. We characterize exact inference as effective descent: local beliefs form a descent datum when compatibility conditions hold on overlaps. This framework unifies tree exactness, junction tree algorithms, and loopy BP failures under sheaf-theoretic obstructions. We introduce HATCC (Holonomy-Aware Tree Compilation), an algorithm that detects descent obstructions via holonomy computation on the factor nerve, compiles non-trivial holonomy into mode variables, and reduces to tree BP on an augmented graph. Complexity is \(O(n^2 d_{\max} + c \cdot k_{\max} \cdot δ_{\max}^3 + n \cdot δ_{\max}^2)\) for \(n\) factors and \(c\) fundamental cycles. Experimental results demonstrate exact inference with significant speedup over junction trees on grid MRFs and random graphs, along with UNSAT detection on satisfiability instances.

Large Causal Models from Large Language Models

We introduce a new paradigm for building large causal models (LCMs) that exploits the enormous potential latent in today's large language models (LLMs). We describe our ongoing experiments with an implemented system called DEMOCRITUS (Decentralized Extraction of Manifold Ontologies of Causal Relations Integrating Topos Universal Slices) aimed at building, organizing, and visualizing LCMs that span disparate domains extracted from carefully targeted textual queries to LLMs. DEMOCRITUS is methodologically distinct from traditional narrow domain and hypothesis centered causal inference that builds causal models from experiments that produce numerical data. A high-quality LLM is used to propose topics, generate causal questions, and extract plausible causal statements from a diverse range of domains. The technical challenge is then to take these isolated, fragmented, potentially ambiguous and possibly conflicting causal claims, and weave them into a coherent whole, converting them into relational causal triples and embedding them into a LCM. Addressing this technical challenge required inventing new categorical machine learning methods, which we can only briefly summarize in this paper, as it is focused more on the systems side of building DEMOCRITUS. We describe the implementation pipeline for DEMOCRITUS comprising of six modules, examine its computational cost profile to determine where the current bottlenecks in scaling the system to larger models. We describe the results of using DEMOCRITUS over a wide range of domains, spanning archaeology, biology, climate change, economics, medicine and technology. We discuss the limitations of the current DEMOCRITUS system, and outline directions for extending its capabilities.

Consciousness as a Functor

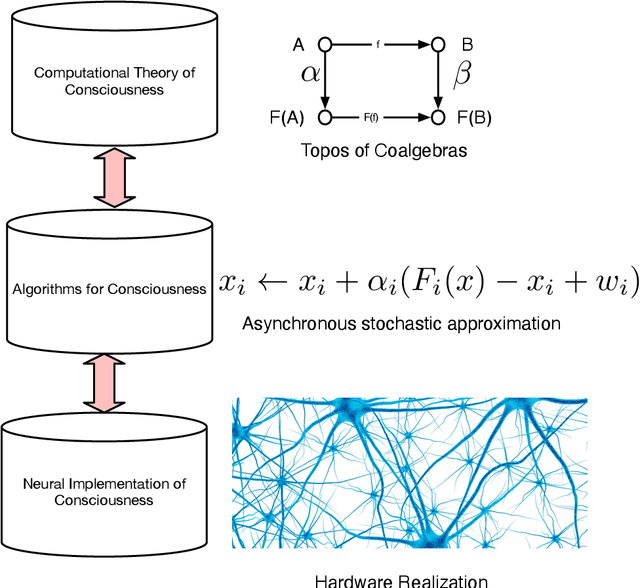
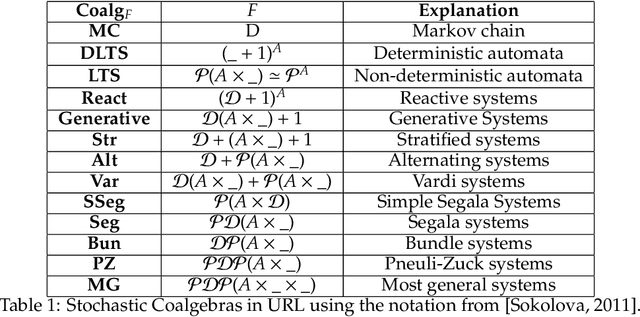
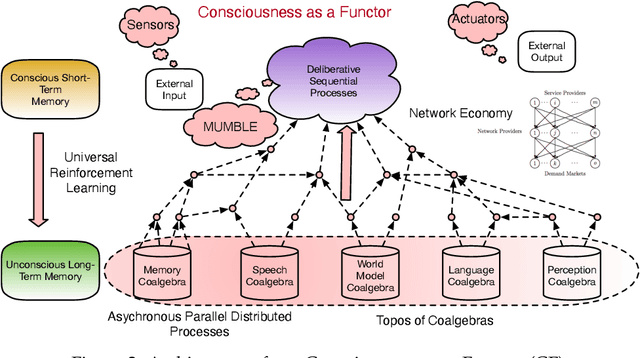
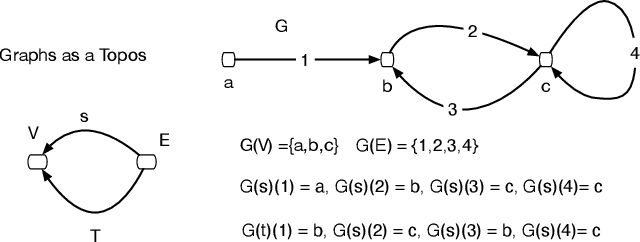
We propose a novel theory of consciousness as a functor (CF) that receives and transmits contents from unconscious memory into conscious memory. Our CF framework can be seen as a categorial formulation of the Global Workspace Theory proposed by Baars. CF models the ensemble of unconscious processes as a topos category of coalgebras. The internal language of thought in CF is defined as a Multi-modal Universal Mitchell-Benabou Language Embedding (MUMBLE). We model the transmission of information from conscious short-term working memory to long-term unconscious memory using our recently proposed Universal Reinforcement Learning (URL) framework. To model the transmission of information from unconscious long-term memory into resource-constrained short-term memory, we propose a network economic model.

Universal Reinforcement Learning in Coalgebras: Asynchronous Stochastic Computation via Conduction

In this paper, we introduce a categorial generalization of RL, termed universal reinforcement learning (URL), building on powerful mathematical abstractions from the study of coinduction on non-well-founded sets and universal coalgebras, topos theory, and categorial models of asynchronous parallel distributed computation. In the first half of the paper, we review the basic RL framework, illustrate the use of categories and functors in RL, showing how they lead to interesting insights. In particular, we also introduce a standard model of asynchronous distributed minimization proposed by Bertsekas and Tsitsiklis, and describe the relationship between metric coinduction and their proof of the Asynchronous Convergence Theorem. The space of algorithms for MDPs or PSRs can be modeled as a functor category, where the co-domain category forms a topos, which admits all (co)limits, possesses a subobject classifier, and has exponential objects. In the second half of the paper, we move on to universal coalgebras. Dynamical system models, such as Markov decision processes (MDPs), partially observed MDPs (POMDPs), a predictive state representation (PSRs), and linear dynamical systems (LDSs) are all special types of coalgebras. We describe a broad family of universal coalgebras, extending the dynamic system models studied previously in RL. The core problem in finding fixed points in RL to determine the exact or approximate (action) value function is generalized in URL to determining the final coalgebra asynchronously in a parallel distributed manner.

GAIA: Categorical Foundations of Generative AI

In this paper, we propose GAIA, a generative AI architecture based on category theory. GAIA is based on a hierarchical model where modules are organized as a simplicial complex. Each simplicial complex updates its internal parameters biased on information it receives from its superior simplices and in turn relays updates to its subordinate sub-simplices. Parameter updates are formulated in terms of lifting diagrams over simplicial sets, where inner and outer horn extensions correspond to different types of learning problems. Backpropagation is modeled as an endofunctor over the category of parameters, leading to a coalgebraic formulation of deep learning.

Zero-th Order Algorithm for Softmax Attention Optimization

Large language models (LLMs) have brought about significant transformations in human society. Among the crucial computations in LLMs, the softmax unit holds great importance. Its helps the model generating a probability distribution on potential subsequent words or phrases, considering a series of input words. By utilizing this distribution, the model selects the most probable next word or phrase, based on the assigned probabilities. The softmax unit assumes a vital function in LLM training as it facilitates learning from data through the adjustment of neural network weights and biases. With the development of the size of LLMs, computing the gradient becomes expensive. However, Zero-th Order method can approximately compute the gradient with only forward passes. In this paper, we present a Zero-th Order algorithm specifically tailored for Softmax optimization. We demonstrate the convergence of our algorithm, highlighting its effectiveness in efficiently computing gradients for large-scale LLMs. By leveraging the Zeroth-Order method, our work contributes to the advancement of optimization techniques in the context of complex language models.

Randomized and Deterministic Attention Sparsification Algorithms for Over-parameterized Feature Dimension

Large language models (LLMs) have shown their power in different areas. Attention computation, as an important subroutine of LLMs, has also attracted interests in theory. Recently the static computation and dynamic maintenance of attention matrix has been studied by [Alman and Song 2023] and [Brand, Song and Zhou 2023] from both algorithmic perspective and hardness perspective. In this work, we consider the sparsification of the attention problem. We make one simplification which is the logit matrix is symmetric. Let $n$ denote the length of sentence, let $d$ denote the embedding dimension. Given a matrix $X \in \mathbb{R}^{n \times d}$, suppose $d \gg n$ and $\| X X^\top \|_{\infty} < r$ with $r \in (0,0.1)$, then we aim for finding $Y \in \mathbb{R}^{n \times m}$ (where $m\ll d$) such that \begin{align*} \| D(Y)^{-1} \exp( Y Y^\top ) - D(X)^{-1} \exp( X X^\top) \|_{\infty} \leq O(r) \end{align*} We provide two results for this problem. $\bullet$ Our first result is a randomized algorithm. It runs in $\widetilde{O}(\mathrm{nnz}(X) + n^{\omega} ) $ time, has $1-\delta$ succeed probability, and chooses $m = O(n \log(n/\delta))$. Here $\mathrm{nnz}(X)$ denotes the number of non-zero entries in $X$. We use $\omega$ to denote the exponent of matrix multiplication. Currently $\omega \approx 2.373$. $\bullet$ Our second result is a deterministic algorithm. It runs in $\widetilde{O}(\min\{\sum_{i\in[d]}\mathrm{nnz}(X_i)^2, dn^{\omega-1}\} + n^{\omega+1})$ time and chooses $m = O(n)$. Here $X_i$ denote the $i$-th column of matrix $X$. Our main findings have the following implication for applied LLMs task: for any super large feature dimension, we can reduce it down to the size nearly linear in length of sentence.

An Over-parameterized Exponential Regression

Over the past few years, there has been a significant amount of research focused on studying the ReLU activation function, with the aim of achieving neural network convergence through over-parametrization. However, recent developments in the field of Large Language Models (LLMs) have sparked interest in the use of exponential activation functions, specifically in the attention mechanism. Mathematically, we define the neural function $F: \mathbb{R}^{d \times m} \times \mathbb{R}^d \rightarrow \mathbb{R}$ using an exponential activation function. Given a set of data points with labels $\{(x_1, y_1), (x_2, y_2), \dots, (x_n, y_n)\} \subset \mathbb{R}^d \times \mathbb{R}$ where $n$ denotes the number of the data. Here $F(W(t),x)$ can be expressed as $F(W(t),x) := \sum_{r=1}^m a_r \exp(\langle w_r, x \rangle)$, where $m$ represents the number of neurons, and $w_r(t)$ are weights at time $t$. It's standard in literature that $a_r$ are the fixed weights and it's never changed during the training. We initialize the weights $W(0) \in \mathbb{R}^{d \times m}$ with random Gaussian distributions, such that $w_r(0) \sim \mathcal{N}(0, I_d)$ and initialize $a_r$ from random sign distribution for each $r \in [m]$. Using the gradient descent algorithm, we can find a weight $W(T)$ such that $\| F(W(T), X) - y \|_2 \leq \epsilon$ holds with probability $1-\delta$, where $\epsilon \in (0,0.1)$ and $m = \Omega(n^{2+o(1)}\log(n/\delta))$. To optimize the over-parameterization bound $m$, we employ several tight analysis techniques from previous studies [Song and Yang arXiv 2019, Munteanu, Omlor, Song and Woodruff ICML 2022].

A Layered Architecture for Universal Causality

We propose a layered hierarchical architecture called UCLA (Universal Causality Layered Architecture), which combines multiple levels of categorical abstraction for causal inference. At the top-most level, causal interventions are modeled combinatorially using a simplicial category of ordinal numbers. At the second layer, causal models are defined by a graph-type category. The non-random ``surgical" operations on causal structures, such as edge deletion, are captured using degeneracy and face operators from the simplicial layer above. The third categorical abstraction layer corresponds to the data layer in causal inference. The fourth homotopy layer comprises of additional structure imposed on the instance layer above, such as a topological space, which enables evaluating causal models on datasets. Functors map between every pair of layers in UCLA. Each functor between layers is characterized by a universal arrow, which defines an isomorphism between every pair of categorical layers. These universal arrows define universal elements and representations through the Yoneda Lemma, and in turn lead to a new category of elements based on a construction introduced by Grothendieck. Causal inference between each pair of layers is defined as a lifting problem, a commutative diagram whose objects are categories, and whose morphisms are functors that are characterized as different types of fibrations. We illustrate the UCLA architecture using a range of examples, including integer-valued multisets that represent a non-graphical framework for conditional independence, and causal models based on graphs and string diagrams using symmetric monoidal categories. We define causal effect in terms of the homotopy colimit of the nerve of the category of elements.